Oak oui google ne m'aide pas trop là. Ils parlent d'un truc pour franchir un fossé.
Merci Tetenbois, je ne connaissais pas.
Du coup, tu as une ouverture en permanence dans l'atelier ?
Ça ne rafraîchit pas trop l'hiver ?
ok merci de ta réponse.
J'envisage peut être de mettre une vmc qui attirerait l'air vers l'extérieur au moment où l'aspi est en marche. A terme, je devrai avoir un peu la même configuration que toi.
j'aime bien dans l'absolu.
Après, est ce adapté ? Sans doute.
Est ce que ce sera utilisé ? Nous verrons.
L'idée était bonne mais c'est pas facile à mettre en image ce genre de choses.
Il a plus de gueule que l'ancien atelier.
Ça doit être agréable d'y bosser !
Ça dépend de ton outillage.
Tu peux les faire à la main.
A la scie à ruban.
A la tenonneuse ou toupie avec une cale pour mettre la traverse penchée et usiner le tenon droit.
A la scie sous table aussi mais ça me parait acrobatique.
Pour 4 tenons, je les ferais à la scie à ruban.
Pour 6 chaises, je ferais sûrement un montage d'usinage à la toupie.
Oui mais tu fais comment pour trouver l'angle de dévers du diamètre vertical ?
Je veux un tracé pour confirmer ! 
Ben oui, il y a de la spéculation dans l'air. Certains se sont préparé des retraites dorées ! 
et encore c'est un 1/2 point technique, pas artistique 
Ce n'est pas là que je l'ai trouvée.
Il y a eu de bonnes propositions même si elles ne marchent pas. (sauf peut être celle de Kentaro).
Ce n'est pas un indice mais il y au moins 11 réponses possibles.
dneis quand le concours sera terminé, ce sera sympa de voir le domaine d'application 
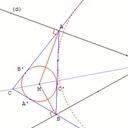
Je précise que les droites et le point M sont totalement aléatoire. Certaines réponses explorent même avec un point M extérieur aux droites (d) et (d').
Boris Beaulant finalement si, il y a en a une voire 2 de trouvées. Mais dans les 11, il y a en a des vraiment compliquées.
Les plus grand noms des mathématiques ce sont amusés là dessus !
Effectivement, j'ai pris bien soin de ne pas utiliser les mêmes termes que le site internet sur lequel j'avais fait cette trouvaille.
C'est "l'intersection inaccessible".
Boris Beaulant oui, c'est ce qui m'a étonné à la base.
Le problème est simple à poser mais plus compliqué qu'il en a l'air.
Et on voit que la ressource en géométrie est infinie ou presque, on arrive à trouver plein de méthodes.
Merci à tous pour votre participation, je ne pensais pas qu'on userait autant nos neurones sur cette question !
Voici le site sur lequel j'ai trouvé le problème et les solutions.
Sauf celle que j'ai proposé dans ma réponse.
debart.pagespe...ble.mobile.html
Le site est franchement bien, pour ceux qui n'ont pas encore mal à la tête vous pouvez aller y faire un tour.
Mais c'est moins marrant qu'ici.
Ça n'empêche pas de continuer à jouer pour ceux qui veulent.
L'approche est originale en tout cas.
On va cogiter ça !
et comme ça ?
(c'est pas de moi)
De rien, je n'ai fait qu'un copié collé d'un site web ;-)
Il n'y a pas de méthode qui utilise une droite quelconque passant par M. J'essaie de tracer ce que tu as décrit pour le confirmer.
Effectivement ça ne semble pas marcher.
- si j'ai bien compris ce que tu voulais dire
- si mon tracé est assez précis, ce qui n'est pas certain
Je n'avais pas vu les commentaires de Kentaro et Boris Beaulant
Du coup ça doit venir de mon tracé. Et si je ne l'ai a
pas dans les méthodes données, c'est sûrement parce que les réponses que j'ai ne se trouvent que par le tracé. Pour certains uniquement à la règle d'ailleurs.
Kentaro au fait, quand tu dis verticale, c'est une vraie Verticale ? avec un V majuscule ? et qui tient debout avec un fil à plomb et tout et tout ?
(j'ai pris une droite quelconque qui va de haut en bas)
Bon, avec des Vraies verticales, ça marche encore moins bien... :(
aucune idée si ta justification mathématique est juste...
oui mais si le rapport du petit côté sur le grand est constant alors le rapport du petit côté sur le tout est constant aussi non ?
ça me simplifiait les calculs ;)
Alors là, j'avoue que je ne sais plus trop. Les tracés simples de géométrie ça va, la trigo un peu et après c'est plus compliqué pour moi. ;-)
OK, c'est ce que j'avais compris au début.
C'est marrant mon premier dessin était très proche avec des quelconques et le deuxième avec des verticales était plus éloigné.
Il faudrait trouver une méthode de report des rapports au compas pour être plus précis. En mesurant, c'est forcément plus imprécis.
Alors ? Ça vous a occupé à ce que je vois.
Kentaro je ne comprends pas ta méthode pour reporter le rapport. C'est la 5 ème figure qui me perd. Tu mets les 2 rapports sur la même verticale ?
dneis oui bien sûr, tu peux y aller 
Kentaro oui il y a plein de méthodes, il faut que je vérifie mais je crois en avoir trouvé une autre
Je te crois... 
et non
(la ligne verticale représente la limite virtuelle de la feuille)
Comme je l'ai dit plus haut, la question du parallélogramme est une bonne piste
Un indice, je crois que ça marche avec des parallèles mais pas n'importe lesquelles...
Boris Beaulant Commentaire du deuxième essai. C'est bien tenté mais il faut rajouter l'étape utilisée par fab83
C'est presque ça.
ben parce que je ne l'ai aps vu dans les 11 méthodes ! Attends, je le trace pour voir
Si je ne me suis pas trompé, ça marche effectivement pas.
Boris Beaulant ah oui, il y a une inversion, tu reportes un point sur la parallèle de l'autre droite... effectivement ça marche.
Je vérifie mais c’est peut être bien la solution par le parallélogramme...
Bien joué (mais faut être tordu )
C'est le "parallelogramme inaccessible de sommet M", wahou !!
Et en fait, le fait de diominuer, c'est le principe de l'Homothétie reprise par fab83.
Ha ha désolé de t'avoir empêché de dormir ^^
Il y avait des méthodes visuellement qui ressemblaient à ça.
J'avoue que je commence à m'y perdre un peu avec toutes ces solutions. On voit que certains on quand même des bons niveaux en géométrie !
pour bien comprendre, ta verticale est quelconque ?
Oui c'est que j'avais cru comprendre, mais je ne voulais pas utiliser le terme de parallèle pour ne pas te donner de piste. Je vérifie ...
Elle est jolie ta proposition, on dirait l'étoile noire !!!
Mais ça ne répond pas à la question (si j'ai bien compris ce que tu voulais dire).
ah oui mais M est donné !
Tu ne vas pas changer le robinet de place parce que ça t'arrange !
eut Bretzel tu traces des novueaux cercles avec pour centre l'intersection des cercles et des droites ? Et en conservant le même rayon ?
Oui très très bien ! Et je ne retrouve pas d'équivalent dans les méthodes trouvées.
bravo !
et ça s'appelle comment ???
(c'est un mot que je connais depuis ce soit même si je crois l'avoir vu pendant ma scolarité...)
En tout cas, c'est une méthode, bravo !
C'est une Homothétie de rapport 1/2 !
Ça fait classe quand même !
On la doit à Michel Chasmes fr.wikipedia.o.../Michel_Chasles
il y a une méthode pour diviser par ce que l'on veut.
Oui mais tu la trouve comment cette "parallèle qui nous intéresse" ?
Oui c'est ça. ça doit être le principe du pantographe
oui mais il faut bien que les 2 parallèles (celle de d et de d') soient tracées sur le même principe.
ah oui, ça carbure là !!!
Wahou !!!! Si je ne fais pas d'erreur, cette méthode s'appelle "la construction par polaires réciproques" !
D'après Jean Henri Lambert 1728-1777.
Well done !!!
Et non ce n'est pas bon non plus (la ligne rouge).
la ligne verticale est la limite virtuelle de la feuille
la droite au crayon de papier est tracée suivant la méthode de Boris Beaulant
ah oui, je 'suis con, j'ai pris la bissectrice de ta proposition... 
Du coup, effectivement, ça marche ! (c'est la ligne bleue).
Effectivement ça peut être en dehors de la feuille.
Bravo à Stef64 et à Boris Beaulant (pour avoir insisté et fait la démonstration)
Oui, la méthode peut marcher dans certains cas, mais pas tout le temps.
Bel atelier, on voit que c'est fonctionnel !
Mais c'est quoi un saut de loup ??