En effet, je n'avais pas lu en détail, mais c'est exactement ce que décrit benjams.
Cependant, en manipulant le solveur graphique, je n'arrive pas à vos conclusions.
En effet, on est coincé si on détermine toutes les positions des points à l'avance. Il faut en laisse une de libre (mais néanmoins positionné sur l’ellipse) pour donner le degré de liberté nécessaire à la résolution.
Je vais essayer de l'expliquer avec mes mots:
Partons du quadrant nord et traçons un arc en direction de l'est avec un point d'arrivée sur l'éllipse. Le centre de cet arc est sur l'axe des ordonnées (l'arc serait donc tangent à son symétrique vertical).
Traçons le rayon entre le centre et ce point d'arrivée.
Tarçons un nouvel arc dont le centre si situe sur ce rayon, le point de départ coïncide avec le point d'arrivée d' l'arc précédent. Rien n’empêche ce rayon d'intersecter l'ellipse. Nous pouvons donc trouver un point d'arrivée sur l'ellipse.
On peut continuer ainsi, mais on ne pourra par rejoindre l'axe des abscisses car dans ma démarche le point d'arrivée de l'arc est un résultat et non un paramètre.
Du coup, pour terminer ma figure, je suis parti depuis le quadrant est. J'ai tracé un arc dont le centre est positionné sur l'axe des abscisses (l'arc est donc tangent à son symétrique horizontal) et le point d'arrivée est sur l'ellipse.
Il suffit ensuite de créer un arc de raccordement dont le centre est situé à intersection du dernier rayon venant du nord et de celui venant de l'est. (triangle jaune).
Ce n'est pas très mathématique comme explication, mais je suis confiant que le fait que ça puisse se mettre en équation.
En fait, la difficulté à la fin c'est d'écrire l'équation du point de rencontre de deux cercles dont on connait :
- Les coordonnées d'un point de "départ",
- L'équation de la droite sur laquelle est situé le centre.
- L'équation de l'ellipse sur lequel est situé le point d'arrivée.
Une autre manière de le résoudre, c'est dire que le point d'intersection entre le dernier rayon (celui qui est flottant) et le rayon de fin d'ellipse est équidistant du point de fin d'ellipse et du point de fin de l'arc précédent.
Bon je vais faire des copeaux maintenant :)
En effet, le cercle n'est pas tangent à l'ellipse. Il est tangent à l'arc suivant.
Ca me semble plus important pour la continuité des surface (au detriment de la précision peut etre)
Au passage, merci pour ton graphique qui est très clair.
C'est vrai que j'avais les problèmes surfaciques en tête, mais il le semble que le souci reste entier en 2D. Si l'export est destiné à un usinage CN par exemple, les discontinuités ont tendance à se voir. Tout particulièrement si la pièce a une finition brillante.
Sur ce, je pense avoir passablement monopolisé l'attention et je suis sûr que vous avez compris mon avis... Et ce n'est qu'un avis.
Je suis certain que vous ferez pour le mieux.
Bonne suite sur ce sujet et bonne soirée pour l'immédiat.
Kentaro c'est vrai. Et comme dans tous les domaines, c'est la simplicité qui fonctionne (et qui est souvent difficile à atteindre).
Je ne sais pas ce qui est le plus simple ici. Aux codeurs de le déterminer.
Pour une pièce a l'extérieur, ce n'est pas dramatique que tes pièces soient rabotées "d'usine". Ça ne devrait pas engendre de problème de géométrie, mais plutôt des problèmes de désafleur... qui apparaitront de toute manière assez probablement avec le temps en conditions extérieures sans emboitement.
Dans le cas présent, j'émettrais un premier doute sur le parallélisme d'avant en arrière des poteaux (coplanaires). Il est difficile à réaliser et aussi à maintenir dans le temps sans maçonnerie ou charpente conséquente. Tu peux le tester en tendant deux ficelles en diagonale des gonds si les ficelles entrent en collision ou au contraire s'écartent au lieu de s'effleurer, c'est que les poteaux ne sont pas parallèles.
A l'inverse, si tu arrives à constater que des vantaux ne sont effectivement pas plans, ça vient surement de la planéité de la surface sur laquelle tu as effectué l'assemblage. Parfois il suffit de poser simplement un panneau et quelques cales judicieusement placées en dessous pour obtenir une surface suffisamment plane (l'horizontalité n'a aucun importance).
Nairod
La vidéo est en effet montée en "va et vient" mais c'est pour des fins artistiques.
Si on ne regarde que la moitié de la vidéo, on observe comment le bois "tire à cœur" puis comment les pièces reprennent à peu près leur géomètrie, mais avec une taille plus petite.
Il est intéressant d'observer que la forme d'une pièce est bien la combinaison de ses tensions internes.
Hello.
J'ai systématiquement depuis 6 jours une erreur 500 lors de la publication d'une trouvaille. Pourtant d'autres utilisateurs ont pu publier des trouvailles... je suis perplexe. J'ai désactivé mon bloqueur de pub, j'ai essayé de simplifier ma publication, rien n'y fait.
OK Boris Beaulant.
Je vais essayer de trouver une solution de contournement.
une image fixe un peu bidon pourrait peut être faire l'affaire.
Pour le coup je vais peut être passer par YouTube ou consort.
Bonne soirée.
Merci trente six seb pour ces explications convaincantes, et pour avoir pris le temps de demander ces infos autour de toi.
J'ai reçu deux nouvelles photos. Je met à jour la publication pour les y inclure.
Bonjour trente six seb
En approfondissant mes recherches, je pense que l'origine bressane n'est pas si évidente car la ronce; absente ici en est un trait caractéristique. Je me demande s'il ne faut pas aller voir chez les voisins de Lyon pour retrouver plus de perpendicularité dans les lignes ainsi que l'usage du noyer massif 'tel quel'.
Pense tu que la sculpture de fleur en traverse basse ait remplacé un ancien motif?
Merci Atelier Eustache ! pour la piste du chrisme. on en est pas bien loin quand meme
C'est très sympa et bien pensé.
Je vois qu'il y en a une série. Tu les vends? Si ce n'est pas indiscret, à quel prix ?
(L'asso des parents d'élève du village est friande de ce genre de réalisation à vendre avant Noël pour financer les sorties du reste de l'année).
Bonjour etiennedesthuilliers . C'est intéressant. Je ne savais pas que les armoires étaient souvent recouvertes.
Néanmoins, vu le positionnement de l'inscription,derrière la traverse basse avant, je ne suis pas sûr que la toile ait un quelconque intérêt esthétique ici. Quelle était sa fonction? une toile de propreté, un peu comme sur les sièges ?
Aussi, j'ai demandé des photos supplémentaires, notamment de la serrure, pour affiner un peu la datation.
Je pensais aussi à un meuble XIXe au début, influencé par la "simplicité" des lignes et détails, mais les fiches me semblent anciennes. Peut être sont elles simplement très rustiques.
+1 aussi
Soit dit en passant, ça peut être assez irritant, voir désagréable.
Bien joué Marc. Ça répond vraiment à une problématique.
Je suis bien content que ça vous soit utile. J'ai encore utilisé la mienne hier en me disant aussi que c'était quand même un progrès :)
J'ai eu un cas similaire et le vitrier m'a conseillé un verre trempé (pas feuilleté) de 6 mm.
En tous cas, c'est effectivement une personne de bon conseil.
Ha tiens, aujourd'hui, je fignolais justement des queues d'aronde avec un de tes ciseaux à douille, et je me disais qu'il était un poil long.
Je vais mettre ce nouveau modèle dans ma liste au père Noël.
Bravo
Oui. Ça fonctionne assez bien. Il y a un coup de main à prendre pour être régulier en vitesse et en pression, mais je doute que ce soit bien mieux avec la version du commerce.
Sur une longueur d'un mètre ou deux, ça va, mais il faudra sans doute à terme que je modifie la buse ou que je mette des déflecteurs.
Oui, une Stepcraft M700
C'est pas mal mais un peu léger quand même pour du bois et des fraises de 8.
Tu devrais gagner 20 kg de masse, et ce n'est pas négligeable je trouve. Je vais essayer de prendre un moment un moment pour simuler le projet avec Structurix. Ça m’amuse et ça m'évite de perdre la main.
A mon avis, ca doit passer. Prenons une table Ikea ou de jardon : 2 tubes un panneau et une portée de plus de 150 cm... et ça tient. Ce serait dommage de mettre un pied au milieu si on peut l'éviter
Bonjour PierreB74,
Je me suis lancé dans ce calcul qui m'a donné finalement pas mal de fil à retordre avec les outils à ma disposition.
Conclusion, le stratifié EP. 0.8 de part et d'autre d'un MDF de 30 mm double sa rigidité. Avec une force de 100 kg au milieu de l'arrondi, en bord de plateau, on a une flèche toute théorique de 136 mm environ.
On aurait une flèche d'environ 20 mm sous son poids propre.
Bref ca mérite quand meme quelques tubes de renfort.
La suite n’intéressera pas grand monde, mais je l'écris pour que mon travail soit vérifiable par des spécialistes.
Voici les détails du calcul:
- Difficulté à trouver les caractéristiques mécaniques du CP. Je suis donc parti sur du MDF (E=2100 MPa, MV=700 kg/m3)
- Caractéristiques mécaniques du stratifié : E=9000 Mpa, MV=1200 kg/m3 mais on part sur la même que le MDF pour simplifier le calcul (l'influence sur le résultat est négligeable
- Impossible de modéliser une plaque de la bonne forme avec Structurix
- Essai de modélisation 3D avec Fusion 360. vu le ratio entre la faible épaisseur du strat et la longueur du panneau, le maillage provoque de gigantesques erreurs de calcul et je n'ai pas le module permettant de modéliser des plaques pour le calcul MEF.
- Il faut donc ruser et voici les hypothèses : tant qu'on ne s'occupe pas de la contrainte, Le couple EI (module d'young - propriété du matériau, et moment quadratique - propriété de la section) est toujours associé dans les formules. Donc si on considère que EI(total) = EI(mdf)+EI(strat) et que EI(strat) = x.EI(mdf), alors, EI(total)=EI(mdf)*(1+x).
Si on calcul séparément les I (on connait déjà les E), on obtient x = 0,72 (je vous passe le détail du calcul : fr.wikipedia.o...ent_quadratique). - J'ai ensuite modélisé la plaque dans le logiciel RDM6, qui malgré une interface d'un autre temps permet pas mal de choses intéressantes. Épaisseur 31,6 mm / E=2100*1,72=3.62 pour obtenir le résultat annoncé plus haut.
NOTA : le rapport entre les couples EI est de 1,72 et le rapport de déformée est plutôt de 2. Cette différence s'explique par la différence d'épaisseur apportée par l'ajout de 2x0.8mm de stratifié.
Voilà le raisonnement est un peu tordu mais je l'ai manipulé dans tous les sens et je n'ai pas trouvé de grosse incohérence. Les puristes me feront remarquer qu'on utilise pas le moment quadratique en flexion plane, mais si on y regarde de plus près, les équations de flexion plane sont un développement de la théorie des poutres en 2 dimensions et ce petit biais me semble acceptable à ce niveau de calcul.
Si quelqu'un à une licence pour un logiciel de calcul MEF avec la possibilité de mélanger des éléments volumiques et plaques, ou de superposer des plaques, je serais curieux de comparer les résultats. Marc Janod si tu nous entends ;)
Arvi
Salut Marc Janod , je vois que tu as encastré les deux cotés. J'ai pris des conditions un peu plus pessimistes. J'ai bloqué les trois déplacements et deux rotations d'un coté (z et y), et de l'autre, seulement le déplacement en z et deux rotation (z et x)
Aussi j'ai mis la charge de 100 kg sur le bord extérieur du panneau.
Aussi, je ne suis pas sur que le maillage 3D soit bien adapté par rapport au calcul des plaques en flexion. Il faudrait comparer les résultats. En tous cas, c'est presque sûr que ça posera problème pour les feuilles de stratifié.
Pour finir, j'ai un v=0.25 au lieu de 0.3, mais j'ai mis cette valeur par défaut, n'ayant pas trouvé de référence.
Salut Marc Janod je n'avais pas vu tes réponses.
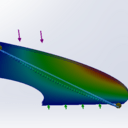
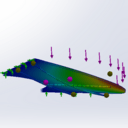
Du coup j'ai moi aussi refait mes calculs, cette fois ci avec Solidworks et un maillage coque.
La première chose très intéressante, c'est que je trouve exactement les mêmes résultats que précédemment, autrement dit, un déplacement d'environ 3 cm sous son poids propre et 13 cm avec la charge de 100 kg répartie sur le bord extérieur (cette fois ci, il y a des visuels, ce sera plus parlants)
Ça me conforte dans mes hypothèses précédentes de modélisation d'un sandwich.
Ensuite on pourrait discuter des déplacements imposé, et on constate avec ton calcul que l'encastrement des deux bout à une incidence majeure sur le résultat. Cependant, je doute qu'elle soit réalisable à cette échelle, le panneau, mesure déjà presque 2,5m dans sa plus grande longueur. On doit pouvoir l'encastrer sur 10 ou 20 cm. dans ce cas, la déformation doit se situer quelque part entre nos deux résultats... mais bon le problème ne se pose plus vraiment.
Par curiosité, j'ai quand même relancé le calcul en activant le mode "grands déplacements" dont RDM6 ne dispose pas et qui semble adapté à la situation et j'ai un déplacement de 198 mm.
Par vice, j'ai aussi lancé le calcul avec un renfort en tube rectangle 40x20x2 et j'obtiens un déplacement sous charge de 100 kg de 44mm.
Et pour terminer en chantant, j'ai aussi essayé la version parasismique, avec une structure en tubes rectangles et j'obtiens un déplacement de 3mm.
Tout ceci me conforte dans l'idée que le pied n'est pas indispensable :)
Sicomin est effectivement un bon fournisseur.
Il y a possibilité de rajouter de la cellulose dans la colle pour la rendre vraiment très forte.
N'hésite pas a consulter les commerciaux, ils sont de bon conseil. La chimie, le collage, l'époxy, ce sont des univers biens particuliers ou il ne faut pas se priver de l'avis de spécialistes.
Bonjour,
Je me permet un commentaire, non pas sur la méthode (je suis dépassé), mais sur la fonctionnalité.
Il me semble très important que les arcs de cercles soient tangents entre eux, au risque de voir apparaitre des bourrelets ou des ondulations. (les amateurs de CAO auront en tête le zébrage discontinu des surfaces)
Autrement dit, que le point de connexion entre deux arcs soit alignés avec les centre des ces mêmes arcs.
J'ai testé avec le solveur de Fusion360 et l'approche ne surcontraint pas la géométrie (les points de connexion sont coïncidents avec l’ellipse)
Sans trop d'assurance, à partir du moment ou vous savez déterminer la position de ces points en fonction de l'équation de l’ellipse, il doit être jouable de déterminer l'équation de la droite passant par le point en question et les deux centres afin de déterminer l'arc suivant. C'est de l’itératif et non de l'analytique me direz vous
Attention toutefois : les positions angulaires des points sur l'ellipse sont interdépendantes. Autrement dit, on ne peut pas compter sur la courbure pour déterminer la position de tous les points. Il faudrait le vérifier mathématiquement, mais avec le solveur graphique je peux fixer la position de tous les points sauf 1, peu importe lequel.