Bonjour tout le monde,
J'ai fabriqué une deuxième table d'appoint, cette fois sur les modèles avec des pieds croisés.
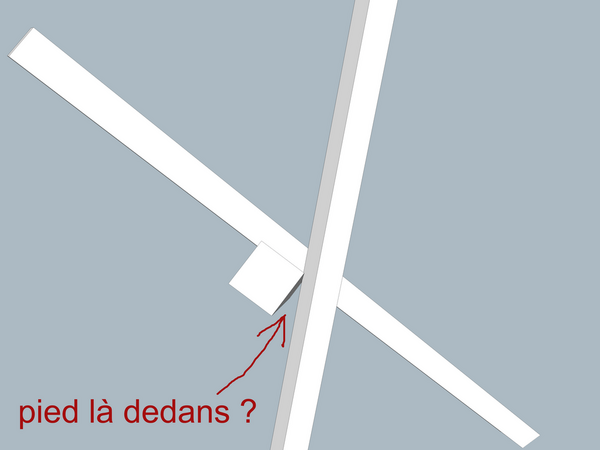
J'ai voulu voir si c'était possible de simplement coller les pieds ensemble, sans structure de support ou emboîtements complexes.
C'est possible ! Ça a demandé une petite tricherie. Voici le détail des chipotes.
Si on simplifie en prenant uniquement 3 pieds de section carrée, il peuvent parfaitement se joindre car chaque pied est à 90° des autres, chacun dans son plan de l'espace.
Le problème c'est que ça donne ça :
C'est très évasé et on manque vite de hauteur utile.
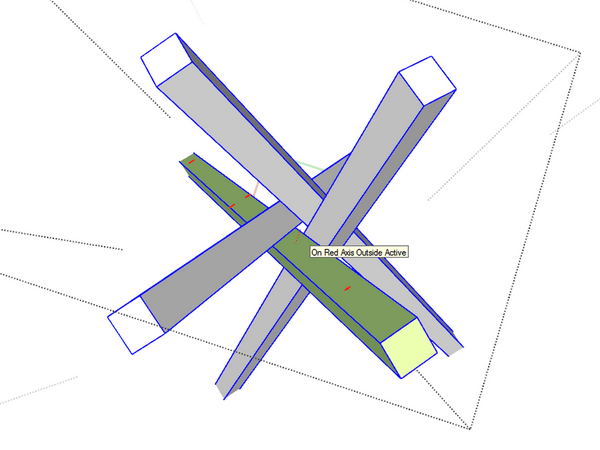
Si on réduit l'angle d'évasement entre les pieds on commence à créer un espace vide. Peut-on y glisser un 4ème pied si on trouve les bonnes inclinaisons ?
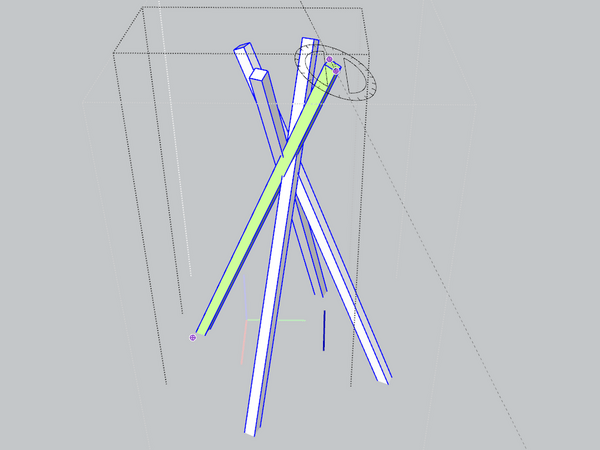
Pour vous donner une idée du contexte, voici le modèle de base pour les chipotes.
Quatre pieds de section carrée et un "angle d'évasement" (à défaut d'autre terme) utile, pas trop aplati :
On peut faire bouger les pieds selon plusieurs axes. J'ai mis un pied en vert comme référence. C'est lui que je modifie et tous les autres suivent par symétrie.
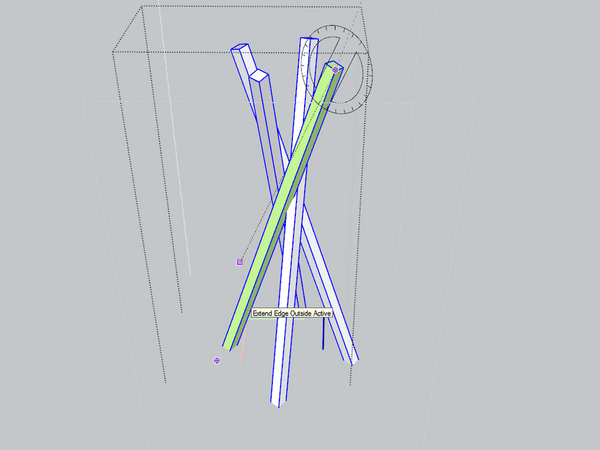
Le premier axe c'est une rotation longitudinale :
Ça aide, notamment pour tenter de mettre les surfaces de contact parallèles.
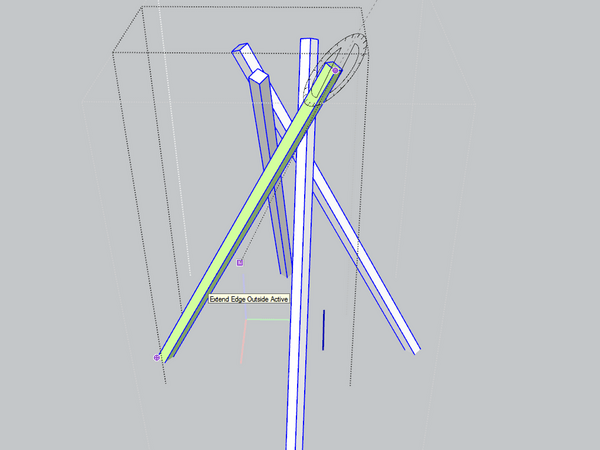
Le deuxième axe c'est une rotation à plat sur un des côté :
Le troisième c'est une autre rotation à plat sur l'autre côté :
Et on peut aussi translationner (c'est un verbe?) dans n'importe quelle direction :
C'est souvent utile pour ramener ensemble les pieds vers le centre.
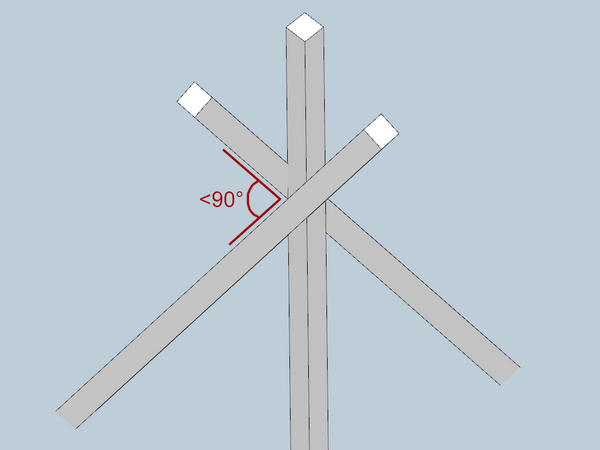
J'ai beau eu modifier tout petit à petit, il m'a semblé qu'une sorte de constante se dégageait : l'angle restant pour la section du 4ème pied ne changeait pas tant que je ne changeais pas l'angle d'évasement de la structure.
Il était toujours inférieur à 90°, ce qui est bien dommage pour tenter d'y coller un pied à section carrée !
Si l'évasement est à zéro degré alors ça marche : c'est jointif mais on a juste quatre pieds verticaux...
Si l'évasement est très faible, genre 14°, ça fonctionne pas mal à un poil près ! Mais la structure globale est trop verticale, pas assez d'appui au sol.
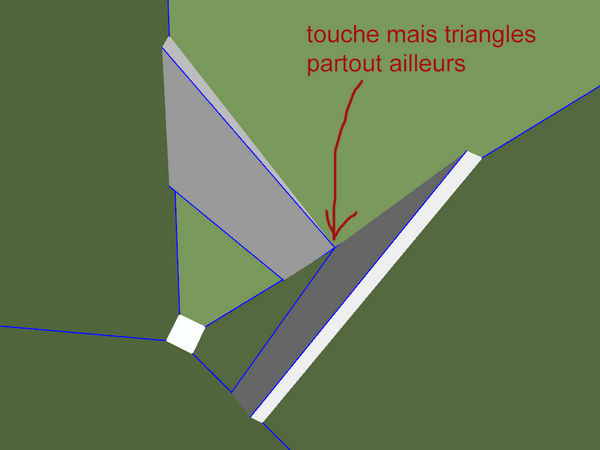
Plus on évase, plus la place restante pour le 4ème pied diminue.
On le voit bien quand on regarde les volumes de collisions à l'intérieur du pied de référence :
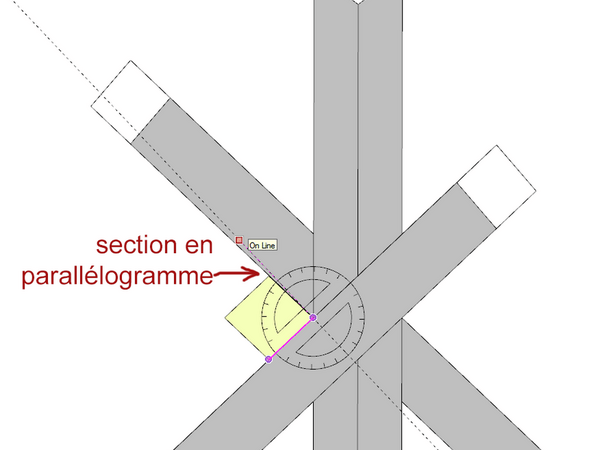
Donc j'en ai eu marre de chercher ce qui me paraissait impossible (la réflexion reste ouverte), et j'ai juste modifié la section des pieds pour un parallélogramme !
Évidemment il ne suffit pas de lui donner l'angle créé par la structure aux pieds carrés, vu que la structure change quand on change la section des pieds.
Après mes ultimes chipoteries, j'ai trouvé un léger parallèlogramme qui fonctionne avec un angle utile d'évasement de la structure globale :
Et j'ai pu fabriquer ma table !
Pour info, à la base j'ai essayé avec 12 pieds, puis 8, puis 6, pour m'arrêter à 4 car assez chiant déjà comme ça. Mais peut-être que c'est possible, avec tricherie ou non, avec un autre nombre de pied. Partagez si vous trouver !
Je suis tombé par hasard sur la création de Kilago par après, mais c'est tellement en lien que je l'ai mise en inspiration.
Voici quelques autres détails de fabrication, en dehors des réflexions SketchUp :
Je vais partager ici les valeurs que j'ai trouvées, comme ça on pourra tous faire des pieds torsadés facilement !
Faut juste que je rentre chez moi d'abord pour pouvoir poster un plan.
[Edit:] Voilà c'est fait :
Merci de m'avoir lu et bons copeaux !
Nairod



























Discussions
Eh béh... À côté de ça, la dernière conjecture de Fermat fait pâle figure !
NB : translater est meilleur que "translationner" !
Ah oui c'est mieux !
Ça a l'air compliqué comme ça mais j'ai juste bougé tout jusqu'à laisser tomber et tricher sur la section
Sinon, il faut apprendre l'art du trait !
Je ne m'y suis pas mis mais c'est tentant
Oulah, je n'y connais rien mais je ne commencerais pas par ça
Comme à ton habitude, c’est très recherché et expérimental


J’ADORE
Merci ! C'était le but, pour trouver une façon d'assembler les sections carrées, mais au final j'ai du faire un compromis.
Ça ouvre des perspectives.

Je ne sais pas si c'est plus facile de faire une section pas carré, ou un usinage pas carré dans des pieds carrés
Couper la section en parallélogramme c'est pas trop compliqué : faut juste pencher la lame. Par contre faut toujours faire gaffe à l'orientation par la suite.
C'est vrai que c'est peut-être plus simple de réaliser l'emboîtement, je n'ai pas essayé.
Merci pour le commentaire !
Nairod Si on reprend ce que j'avais fait en m'inspirant de Sylvain,
et si on ne veut pas faire l'encoche, on s'aperçoit qu'il suffit que les 4 pieds aient une section en forme de trapeze. Sur l'exemple donné, la section fait 100 x 100 et 67 sur le 3ième coté.
Par contre l'intérêt de l'encoche dans le Buenos Aires, c'est que cela bloque les pieds, donc plus solide qu'un simple collage face contre face.
Ah magnifique ! Je ne suis pas sûr de voir le trapèze par contre, et je ne comprends pas les dimensions ?
Autre chose : un trapèze on voit fort que c'est pas une section carrée. Sur ma petite table c'est difficile à deviner, le parallélogramme est tellement léger qu'on dirait un carré. Ça peut être intéressant.
Le collage en bois de fil est étonnamment solide mais évidemment faut pas faire une table à manger avec ça. Pour un gros meuble, un assemblage et des grosses sections me paraissent indispensables.
Nairod Pour le trapèze, sur ce dessin, tu vois la section carrée, et si on rabote la face haute en biais, 100 d'un coté, 67 (100-33) de l'autre, on a alors une section en trapèze
Kentaro Ok je pense que je vois. Un trapèze rectangle.
Est-ce que couper la même section sur les 4 pieds risque de modifier l'angle total dans ton cas ? Il me semble que non...
Sinon j'aurais pu couper une section en trapèze rectangle aussi, en mettant l'angle droit dans le coin de la section qui ne touche rien, mais c'était plus facile de faire un parallélogramme et ça autorise plus de symétries pour positionner le bois autrement si besoin.
Tiens tiens, tout à l'heure je suis passé ici...
Haha, joli ! Je me serais sûrement arrêté
manque plus que l'assise ;-)
Si jamais tu as accès à Rhinoceros3D, j'ai fait un module Grasshopper (le plugin paramétrique) qui permet de faire des tréteaux de Buenos Aires avec plein de pieds, hauteurs variables et compagnie, et on peut extraire le développé des faces pour en faire une fiche de taille.
Avec éventuellement plus que quatre pieds ?
Oui ça m'intéresse, j'ai vu qu'on peut tester la version gratuite. Je t'envoie un MP.
Excellent. Très beau design épuré, j'aime beaucoup.
Et merci pour le partage de réflexions !
Merci ! Oui je dois encore poster les explications, mais j'ai eu la tête ailleurs
Voilà j'ai posté le plan :
Bon Nairod j'ai travaillé pour toi ! Comme je m'en doutais, la sculpture d'Illzach a tous ses carrelets qui se touchent correctement, et ils sont de section carrée.
Donc l'idée, c'est de t'affranchir des symétries et de l'idée qu'ils se touchent tous au même endroit pour te redonner des degrés de liberté.
Ara Très intéressant ! Merci pour la recherche.
Je pense comprendre au moins une partie de la structure, et il me semble effectivement qu'il y a moyen de faire quelque chose en laissant tomber l'idée qu'ils se touchent au même endroit. Et peut-être qu'on peut quand même garder une forme de symétrie.
Petite note : la symétrie combinée avec les points de contacts rapprochés, ça renforce quand même. Maintenant c'est l'avantage d'une table d'appoint : les contraintes sont faibles donc on peut jouer plus.
Une autre chose possible ça serait de partir en live, sans symétrie, avec un aspect fouilli, comme l'artiste a fait avec cette sculpture, mais ça moi je sais pas trop faire.
L'avantage, c'est qu'avec des carrelets en bois de 80 cm, ce sera plus facile à manipuler en live que des barres d'acier de 6m !
Ara Effectivement c'est presque plus facile de tester en vrai, faut juste de la colle qui peut s'enlever. Peut-être colle chaude...
Bon si je poste un truc fouillis plein de colle chaude qui déborde, je compte sur vous pour me remettre sur le droit chemin hein
Ara Je viens de tester et je pense que quelle que soit la configuration, on ne peut jamais recoller à plat le 4ème pied au 1er dès qu'on pivote les pieds (ce que j'appelais "l'angle d'évasement").
C'est pas un problème en soi mais on doit laisser tomber l'idée de "cerclage", de continuité dans le collage (pied 1 collé à 2, 2 collé à 3, 3 à 4 ET 4 à 1). Et donc perdre encore beaucoup en solidité.
La section en parallélogramme autorise ce cerclage car elle vient compenser le léger angle qui se crée entre les faces des pieds quand on les pivote.
Je vais continuer à chipoter un peu sous SketchUp quand même...
Oui mais qui a dit qu'il fallait 4 pieds ? Dans la sculpture il y en a 7... il faut voir le nombre minimal de pieds pour connecter le dernier au premier. Quand j'étais jeune j'avais des cours de recherche opérationnelle, c'était typiquement le genre de trucs qu'on faisait (enfin que le prof nous montrait !).
Après le test de Nairod, nous allons avoir le théorème de Nairod (ou la conjecture, si tu as une marge de bouquin sur laquelle l'énoncer...).
Ara Héhé c'est exactement ce que j'étais en train de tester avec SketchUp :
On crée un défaut de parallèlisme entre les dernières faces à coller quand on donne un évasement aux pieds, quand on les pivote quoi, à cause des angles composés qu'on introduit.
On peut compenser ce défaut de parallèlisme final en trichant sur la section, comme j'ai fait pour ma table.
Mais, ô grande question, peut-on le compenser en augmentant le nombre de pieds ?
On sait déjà que c'est possible en diminuant le nombre de pieds : avec trois pieds de section carrée, chacun dans leur plan, on rempli la condition "cerclage" et en plus y a une symétrie globale dans la structure.
J'avais déjà chipoté avant, et je viens de continuer maintenant, et je commence à vouloir jeter l'éponge pleine de sueur de cerveau parce qu'elle devient un peu dégeulasse.
Ara J'ai testé avec 8 pieds, au cas où doubler fonctionnerait. J'ai choisi un angle d'évasement arbitraire de 22.5°.
Sans fonction paramétrique dans SketchUp pour le modifier l'angle sur toutes les jonctions d'un coup j'abandonne ici.
Voici donc la conjecture de Nairod, que j'invite quiconque avec un meilleur logiciel 3D (ou des connaissances en géométrie) à prouver ou infirmer :
Dans un espace euclidien à trois dimensions parce-qu'on-fait-de-la-menuiserie-faut-pas-déconner, il n'existe pas de nombre de pieds N>3 qui satisfasse les conditions suivantes : section carrée, cerclage du collage (rigoureusement défini ci-dessus), symétrie en rotation de la structure.
Jeter l'éponge, à deux doigt de révolutionner le monde de la sculpture, du bois, de la création et des mathématiques ? Bref, à deux doigt du prix Nobel, tu n'y penses pas sérieusement j'espère !
Ara J'insiste sur la symétrie en rotation sinon on peut créer des structures comme celle ci-dessous, réminiscente de la sculpture du rond-point en fait :
Ara J'aurais voulu un whisky d'abord