Merci Chaluthier !
Si j'ai bien compris voici le plan qui correspond à ta proposition?
Ce n'est pas encore la solution que je cherche, pour plusieurs raisons :
- si j'ajoute une façade sur le meuble vert, je ne pourrai plus incorporer la grande étagère mobile dans le caisson
- ça m'embête de faire des grosses percées sur le meuble bleu, car il peut être utilisé seul
- dans l'idéal j'aimerai que les 2 meubles soient solidaires, même en mouvement vertical
- et puis surtout la découpe des pièces et des trous doit être très précises pour que tout soit calé parfaitement.
Merci pour tes recherches ça me donne aussi de nouvelles pistes de réflexion
Salut Kentaro,
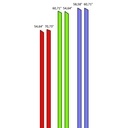
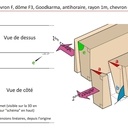
oui sans problème, voir img 4. Ce sont les valeurs pour R=1, à multiplier donc selon le rayon de notre dôme. Après je sais pas si c'est très lisible, le plus simple à mon sens est d'ouvrir le dessin sur Sketchup, faire un facteur d'échelle sur le dôme, selon le rayon qu'on veut et on aura directement les longueurs souhaitées.
Je remets les img 2 et 3 avec la précision sur la position des A et A', B et B'... sur la structure.
Bonjour! Pour l'instant j'ai construit des dômes avec connecteurs, mais à terme j'aimerai expérimenter les dômes en Goodkarma sans connecteurs oui.
Le dernier que j'ai fait était en chêne avec des connecteurs en contreplaqué, et ça me plait bien comme ça. Mais les Goodkarma ont aussi leurs avantages.
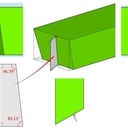
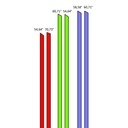
Je suis d'accord. Pour l'angle de coupe de l'extrémité des chevrons B par exemple, il y a l'angle de 60,71° (comme indiqué dans img 3), mais aussi l'angle du boit de bout : 96.79° (voir img 5).
Je pense qu'on pouvoir retrouver toutes ces valeurs sur Acidome (lien fourni par Remi25 dans une autre discussion : lien)
Le plus simple pour moi est d'utiliser le plan 3D et de prendre les cotes et les angles directement dessus.
Salut, Lyveus ,
Aucun problème pour reprendre un sujet d'il y a quelques mois.
Je vois 2 solutions à ta question : soit on utilise un calculateur comme acidome, qui nous donne toutes les infos d'angles et de cotes (voir l'image jointe pour comprendre à quoi correspondent les valeurs d'acidome), soit on le modélise en 3D (par exemple sur sketchup) et on cote pour avoir les mesures.
Lyveus Haa OK. Et bien à ma connaissance non il n'y a pas de formule unique pour le bois car les propriétés mécaniques sont très différentes d'une essence à une autre, selon le séchage etc... Pour d'autres matériaux on peut utiliser des abaques de charges admissibles (alu, acier...), peut-être en existe t-il par essence de bois mais je n'en ai pas connaissance (ça m'intéresserait beaucoup d'ailleurs).
Pour répondre à ta question, si ton dôme est en fréquence 2, les longueurs max font 90cm environ. D'après les constructions que j'ai déjà réalisées, je dirais qu'une section de 10cm² environ serait suffisante. Après ça dépend du bois, et de l'usage (si on suspend des choses ou pas...).
Salut Lyveus. Je n'ai pas fabriqué de dôme en Goodkarma, je n'ai étudié que la conception, je ne pourrai donc pas te répondre sur la partie fabrication.
Mais la méthode de construction que tu décries me parait bonne, faire un gabarit sur un panneau et puis assembler les 3 arêtes.
Je remarque sur ton image que tu utilises la méthode Kruschke, qui permet d'avoir une base de dôme plane en F3, cela ajoute des types de longueurs différentes, dans ton exemples, on a 9 types d'arêtes différents.
Ma méthode est de dessiner en 3D sur sketchup mon modèle de dôme, et de reproduire dans l'atelier selon les cotes mesurées sur mon dessin. Si ça colle pas, comparer le dessin 3D au réel.
Bon courage pour ta fabrication!
Salut Birouf, désolé je viens juste de voir ton commentaire.
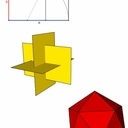
Pour moi la base du dessin est le solide de base qu'on utilise, très souvent l'icosaèdre. Je n'ai pas de tuto mais je peux te dire : pour dessiner un icosaèdre, tu commences par dessiner un rectangles d'or. Ensuite copie/colle le même que tu tournes à 90° horizontalement et verticalement, et un 3ème avec encore 2 rotations à 90°. Tu devrais obtenir l'image 6 jointe. De cette figure il ne reste plus qu'à relier tous les sommets, et POUF voilà un icosaèdre, soit un solide à 12 sommets, 20 faces équilatérales.
C'est lui qu'on utilise pour la grande majorité des dômes géodésiques.
Ensuite si on divise chaque arête de cet icosaèdre en 2, on obtient un fréquence 2, en 3 un fréquence 3 etc... Quand on divise une arête, il faut toujours ramener le nouveau sommet créé à R (rayon) du centre du volume, de sorte que tous les sommets (anciens et nouveaux) soient tous à la distance R du centre.
Sinon tu peux aussi utiliser mon dessin : un facteur d'échelle pour obtenir la dimension de dôme que tu souhaites (sur le dessin R=1m). Tu peux aussi modifier les sections des arêtes du dôme en modifiant les sections des composants F3A, F3B et F3C du dessin. Quelques connaissances Sketchup sont nécessaires pour cette dernière opération.
J'espère que tu trouveras comment concevoir ce que tu souhaites!
Aie décidément j'ai encore laissé passer un mois avant de voir le dernier commentaire, désolé Thierry.
Alors pour répondre à ta question : je n'ai pas pris différentes sections de traverse, j'ai juste expliqué la différence entre 2 techniques : soit on prend des section rectangulaire et on aura des petites différences d'arasements sur les sommets, soit on prend des sections trapézoïdales et on aura des sommet bien pointu bien propres.
Salut Chen,
Comme d'hab un mois plus tard je découvre la notification ! ;)
Oui c'est tout à fait normal, en F3 il n'y a pas d'équateur bien horizontal, donc la base n'est pas tout à fait plate.
En effet un morceau de bois permet de compenser ce petit écart (voir pièce jointe).
Depuis j'ai découvert la méthode Kruschke, qui permet d'avoir une base bien plate, avec des longueurs de bois légèrement différentes (et 4 sections différentes au lieu de 3).
Salut Nico,
Oui c'est tout-à-fait ça!
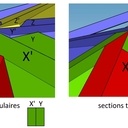
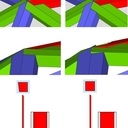
Pour dire autrement, sur l'image jointe (img 10) dans le premier cas les sections des morceaux de bois sont rectangulaires et X et X' ne sont pas tout à fait dans le même plan, de même que Y et Y', Z et Z'. Par contre X' et Y sont dans le même plan, de même que Y' et Z...
A l'inverse quand on a des sections de bois trapézoïdales, alors X et X' sont dans le même plan, de même que Y et Y', Z et Z'... et c'est plus propre pour poser des plaques ou autres sur les triangles
Salut Gugus33. Et non je n'ai pas de formule, je dessine sur sketchup et je regarde ensuite combien font les angles.
Mais sur mon dessin tu peux faire un facture d'échelle du dôme ( x le rayon de ton dôme) et ensuite tu modifies les dimensions des chevrons pour correspondre à ce que tu as.
Salut Lulu, merci pour ton message.
Dslé je n'ai pas compris ta question, peut-être avec un schéma?
Salut Steph,
Wow super projet!
Question 1/ : alors sur le site Acidome, la construction des dômes se fait avec des chevrons rectangulaires, et non trapézoïdaux. On peut le vérifier en téléchargeant le fichier .obj (en haut à droite de la page du site) et en l'important dans Sketchup (il faut une extension "OBJ importer").
Mais ils indiquent quand même la valeur de l'angle e si jamais on souhaite faire la coupe pour avoir des chevrons trapézoïdaux j'imagine.
Question 2/ : effectivement l'indication de l'angle e n'est apparemment pas du bon côté. Il y a peut-être quelque chose qui m'échappe, mais en dessinant la 3D tu verras qu'il n'y a pas de confusion possible, c'est le côté qui est en contact avec le triangle voisin.
Question 3/ : oui bien-sûr, plus la longueur de ton chevron est grande, plus la section doit l'être aussi. Mais il n'y a pas de règles générales étant donné que cela dépend énormément de l'essence du bois, de ses défauts, de son séchage, de ses caractéristiques quoi, et puis de l'utilisation de ton dôme (si tu y accroches des objets, des hamacs... ou pas). Enfin si, il peut y avoir des règles générales, sous forme de de tableaux d’abaques en résistance des matériaux par exemple, mais j'en sais pas plus.
Le petit dôme que tu vas faire, c'est quel diamètre? Et en fréquence 3?
Salut sebb85,
Alors c'est un problème qui revenait régulièrement à l'époque, comprendre à quoi correspondent les valeurs indiquées sur Acidome. Beaucoup de gens se posaient des questions. J'avais fait un schéma pour faire le lien entre les valeurs indiquées dans Acidome et les angles sur une vue 3D.
Je t'avoue que ça fait un bon moment que je n'y suis plus retourné. Et en fait mon plan Sketchup m'allait très bien, alors je n'utilisais plus Acidome.
La seule chose que je puisse te dire aujourd'hui, c'est que si tu as bien dessiné ta 3D sur Sktechup, il n'y a pas de raisons que ça ne fonctionne pas dans la réalité. Jpeux pas plus.
Bonne construction!
Victor
Waow, super ta maquette! Oui la méthode kruschke est vraiment meilleure. Je viens d'ajouter un fichier sketchup avec la 3D pour le F3 kruschke.
En F3 classique tu as 30 triangles AAB et 75 CCB,
En F3 kruschke tu as 30 triangles AAB, 35 CCB et 40 CCD. Donc en effet un type de triangle en plus mais ça vaut le coup.
J'espère que le fichier te sera utile
Bonne journée
Ara pas besoin d'être irréprochable pour donner son avis. Moi je trouve que Tesla est une entreprise qui contribue à la destruction du vivant et de la planète, alors je comprends la question de jepierre
bisous
Salut Tistou, bravo pour ce bel ouvrage, c'est très cool!
Remarque sur la terminologie : sauf erreur de ma part, ton dôme est un F3 (5/8) auquel tu as enlevé quelques triangles.
Sinon je rejoins Kentaro sur le point de vigilance des pieds. Normalement sur un dôme plein tous les sommets ont 5 ou 6 arêtes, 4 pour la base. Il faut éviter au maximum les sommets à 3 ou 2 arêtes.
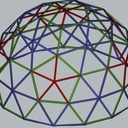
Le risque sur ton dôme est que le triangle formant le pied rotationne autour de l'arête supérieure comme une charnière (voir traits rouges sur l'image jointe). J'ai simulé la pire situation, où les arêtes rotationnent ou cassent, les pieds glissent...
En reformant les triangles enlevés tu améliores le pb mais le risque est toujours présent (voir img 2).
Du coup il me semble qu'il est important de bien se questionner sur qu'est-ce qui empêche (ou pas) les pieds de rotationner en cas de sollicitation?
Pour le vent, effectivement les dômes géodésiques ont une géométrie parfaite pour résister au vent, mais à condition qu'il puisse "glisser" sur la structure et qu'il n'y ait pas d'ouverture dans laquelle il puisse s'engouffrer.
Merci pour le pas à pas à venir!
Bonjour!
Je suis aussi en train de m'intéresser au mode sans connecteur Goodkarma.
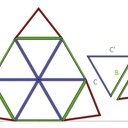
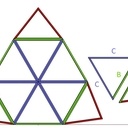
Voilà ce que j'en ai compris : en F3 il y a 2 types de triangles différents : des AAB et des BCC (voir img1 et img2).
Je pensais initialement qu'il y avait un A, un B et un C, en réalité en dessinant sur Sketchup je me suis rendu compte qu'il y avait 2A, très légèrement différents l'un de l'autre, 2B, et 2C. Ils n'ont pas exactement les mêmes dimensions, ni les mêmes angles (voir img3). Du coup si on veut éviter les petits décalages à la construction je pense qu'il faut tenir compte de ces différences (en arrondissant les décimales au demi-degré par exemple). Et du coup fabriquer un gabarit pour AAB et un autre pour BCC.
Je me suis inspiré de la vidéo partagée par Rémi25 pour dessiner le dôme sur Sketchup, ça marche très bien. Je la partage pour ceux·celles que ça intéresse : lien
Victor
Remi25 Oui je me suis interrogé plusieurs fois sur le sens des valeurs indiquées sur acidome pour les montants en Goodkarma, je ne comprends pas à quoi font référence certaines valeurs. Du coup sur Sketchup c'est plus concret pour moi :)
Remi25
Ça y est je viens de comprendre (enfin) comment fonctionne le calculateur Acidome. Et pourquoi je ne pouvais pas retrouver les mêmes valeurs que sur ma 3D : la construction du modèle est différente : sur Acidome la section des chevrons est rectangulaire, tandis que sur mon dessin les sections sont trapézoïdale. C'est plus compliqué à fabriquer mais on obtient des triangles bien plans et des sommets propres. (voir img 6).
Selon les cas l'un et l'autre doivent avoir des avantages et inconvénients.
Salut Olivier Delayen ,
En fait cela dépend de la façon dont on dessine notre modèle. Si tu dessines les chevrons en section rectangulaire, tu devrais obtenir les mêmes valeurs qu'Acidome. J'ai fais le test avec un dôme F3 et je trouves les mêmes valeurs.
Comme précisé sur l'img 6 de mon message précédent, on aura pas tout à fait la même forme, ça dépend si tu veux poser des plaques sur tes triangles par exemple, je pense que les sections trapézoïdales sont plus adaptées. Si tu veux construire un dôme recouvert d'une toile, les sections rectangulaires peuvent convenir et la fabrication sera plus rapide.
J'ai le plan Sketchup en F2 et F3 des 2 façons de faire si ça t'intéresse.
Olivier Delayen
Bonjour,
Oui avec plaisir, je ferai ça à mon retour de vacances (mi-août)
A +
Olivier Delayen
Salut Olivier, j'ai fait une mise à jour de mon plan avec la version en fréquence 2 (lien)

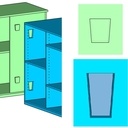









S'il n'y a que 4 petits trous ça n'est pas très grave pour le meuble bleu seul je peux les laisser apparent.
Du coup ta proposition c'est à peu près ce que j'avais imaginé, avec les rails en plus.
Merci Jean-Claude!