Bonjour,
Voici une question de charpente.
je viens d'acquérir le guide suivant :
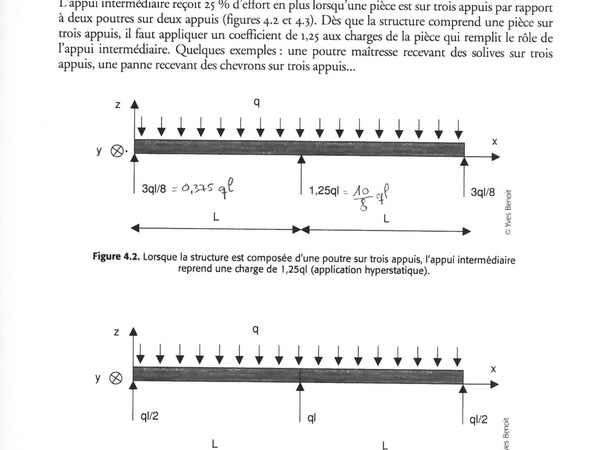
Dans l'introduction sur le calcul des charges (p. 41), il y a ce cas qui décrit la différence à faire lorsqu'on veut dimensionner une poutre sur 3 appuis ou sur 2 appuis :
Dans le cas d'une pièce sur 3 appuis (fig. 4.2), on constate que l'appui central doit supporter 1,25 charge (10/8e de la charge), soit beaucoup plus que les appuis latéraux qui ne supportent chacun que 0,375 charge chacun (3/8e).
Alors que si l'on utilise 2 pièces au lieu d'une seule (fig. 4.3), les charges sont réparties de manière plus équitable : 1 part (8/8e) sur l'appui central, et 1/2 part (4/8e) sur chaque appui latéral.
Dans l'optique de limiter la section (et donc le prix) des éléments porteurs (les appuis), il semble donc plus intéressant de diviser les éléments portés en plusieurs pièces (2 pièces pour 3 appuis) plutôt que d'avoir une grande pièce portée sur plusieurs appuis, car l'élément porteur (appui) pour 1 grande pièce doit pouvoir supporter plus de charge ("1,25") qu'un élément porteur (appui) qui recevraient 2 pièces ("1" charge) : voir l'image d'illustration pour bien comprendre la logique peut-être peu intuitive à la lecture seule.
Cependant cela implique de réfléchir différemment à la fixation des éléments entre eux, notamment en terme de risque d'écartement (longitudinal) ou de glissement (latéral). Je pense particulièrement à l'assemblage éventuel des deux pièces qui sont dans le prolongement l'une de l'autre.
Que ce soit pour une solive de plancher portée par des poutres ou pour une panne portée par des fermes, quels autres éléments de réflexion seraient à prendre en compte pour décider de la stratégie à adopter ?
d'avance merci pour vos éclairages
Florent
6 réponses
Autre chose à prendre en compte:
En effet diviser les éléments portés en plusieurs pièces permet de gagner sur l'élément porteur.
Cependant, la section de l'élément porté pourra être réduite s'il est en une pièce sur trois appuis plutôt qu'en deux pièces (comparer par exemple les tables p.74 et p.78 de ton bouquin).
On gagne d'un côté ce qu'on perd de l'autre, la stratégie optimale dépend de chaque configuration!
Et dans le concret, elle est souvent guidée par les sections que l'on sera en mesure de trouver sans trop de difficulté.
Bonne journée
Je suis quasiment dans une configuration similaire, c'est à dire une grande portée entre deux murs au environs de 8.88 m et implicitement des poutres assez longues.
J'ai une bâtisse de 22 m de long qui a été transformée / modifiée à plusieurs reprises par "des artistes" incompris des années 65.
Par exemple pour une pièce de 64 m² j'ai trois poutres en résineux qui sont comme des cure-dents et assez en mauvais état, sans parler d'un bricolage fait par les "artistes" de l'époque qui n'a fait que les rendre plus fragiles qu'elles ne l'étaient déjà.
Enfin pour parfaire le tout il y a un étage qui a été bâti sur des poutres destinées à la base au grenier, donc nullement prévues pour supporter la charge d'un étage d'habitation.
Mon approche est la suivante :
1 - Sur les grands volumes j'ai mis des poutres en chêne pour réduire les entre axe entre deux poutres qui des fois sont à 3.48 m
2 - Sur les secteurs plus petits je vais rajouter des solives / poutres à demi-largeur de la pièce et monter en HEA / HEB qui va reprendre autant les appuis des "demi-poutres" que les relais de charge pour les poutres longues déjà posées.
Donc je suis dans le cas ou j'ai exactement l'exposé du bouquin une poutre longue travée avec 3 appuis (HEA / HEB et murs) et des poutres à mi-largeur un appuis sur un mur le deuxième sur le HEA / HEB.
Cela fait un peu de calculs à faire sur Excel, cependant pas impossible de le faire et surtout bien définir les sections des éléments bois et des éléments métalliques nécessaire.
Pour ce qui est de la charge repartie en 3 appuis c'est surtout les moments fléchissant qui font que la charge en appui central est plus importante que sur les appuis périphériques.
Cependant la 1.25 ql prise en compte sur la charge à supporter par le HEA / HEB il suffit juste de dimensionner la poutrelle métallique pour la charge résultante afin de supporter le poids.
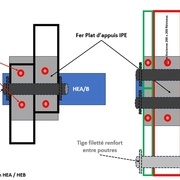
Pour ce qui est de raccords des demi-poutres que je vais installer il a des sabots spécifique pour une prise dans les ailles des poutrelles métalliques et un vissage sur les éléments bois. Par ailleurs dans mon cas les extrémités sont fixe dans les murs et les milieux sont passepoilés et fixes entre eux par des tiges boulonnées et des éléments de fixation prévus pour les HEA évitant ainsi les basculent et/ou la translation des poutres bois.
Désolé pour cette longue réponse mais je voulais exemplifié par un cas concret.
Je ne suis pas charpentier.
Un bâtiment de cette taille, ça ne s’improvise pas, ça se calcule par un bureau d’étude bois.
Ceci dit, je sais qu’il est nettement plus facile d’obtenir une grande résistance à la compression (pour la reprise de charge) pour un appui qu’une grande résistance à la flexion pour une poutre.
Par ailleurs, le raisonnement sur l’appui central est incomplet : en effet, la divion d’une poutre simple en deux poutres ne change pas le poids total statique à supporter.
L’appui terminal porte une demie poutre alors que l’appui central doit porter la demie poutre de gauche et la demie poutre de droite. Il est donc nécessairement plus costaud que les appuis d’extrémité.
Par ailleurs, l’assemblage de deux poutres au-dessus de l’appui central est plus complexe et coûteux qu’une fixation d’appui simple.
Enfin, la résistance à la flexion de l’ensemble de la poutre est meilleure avec une poutre unique.
Bref, je ne vois pas où l’est l’avantage technique de diviser ses poutres (à part des considérations de disponibilité de certaines longueurs ou de contraintes de mise en place selon les moyens de levage ou de prix).
1- Attention, dans le cas 1, si l'appui central supporte 1,25q, les appuis aux extrémités n'ont à supporter que 0, 375d.
Donc, certes, l'appui central doit être plus "fort", mais on gagne sur les deux autres appuis.
Au final, pas certain que l'un ou l'autre solution soit plus "économique".
2- D'autre part, je suis très intéressé à voir les éléments de démonstration et de calcul permettant d'obtenir ces résultats.